Compte-rendu de l'Atelier 3
| La Géométrie actualisée à la portée de TOUS |
UVGT - Unité de Valorisation de la Géométrie des Transformations - asbl |
|
« Raisonner grâce aux polyèdres » (JA20). L'atelier "Raisonner grâce aux polyèdres" (JA20) prévoyait les six thèmes suivants:
Par manque de temps, seuls les thèmes (1) et (2) ont été développés Thème 1. Au cours du premier thème « DETERMINATION DU NOMBRE DE FACES, D’ARETES ET DE SOMMETS D’UN POLYEDRE », nous avons montré et expliqué que les conditions nécessaires (non suffisantes): "Toutes les faces sont des polygones" et "Toutes les faces sont planes", ne sont pas équivalentes pour définir la notion de polyèdre. |
|
|
En effet, depuis les années 1920, les Anglais PETRIE et COXETER ont mis en évidence l'existence de polyèdres formés uniquement de polygones gauches (non coplanaires).[Léonard de Vinci avait déjà présenté des dessins de polyèdres composés de faces planes et de faces gauches.] |
Nous avons présenté les polyèdres
de PETRIE déterminés à partir des cinq polyèdres platoniciens et formés de
polygones gauches réguliers.
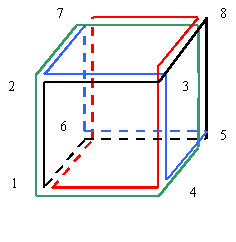
Le fameux "cube" à faces gauches (non planes) de PETRIE (ci dessous)
est déterminé par quatre hexagones gauches réguliers.
 |
Ce sont les 4
hexagones réguliers suivants:
L'hexagone rouge ( 7 - 8 – 3
– 4 – 1 - 6 ) |
|
|
Si ce type de polyèdre peut paraître surprenant, il vérifie néanmoins les caractéristiques habituelles des polyèdres usuels. |
| Les photos
ci-dessous illustrent les autres polyèdres de PETRIE (réalisés en
pailles), associés aux autres polyèdres platoniciens.
Pour reconnaître les polygones gauches réguliers intervenant dans les polyèdres de PETRIE, il suffit de suivre les pailles de la même couleur. |
| Tétraèdre de PETRIE formé de trois quadrilatères gauches réguliers. |  |
|
|
Octaèdre de PETRIE formé de quatre hexagones gauches réguliers. |
| Dodécaèdre de PETRIE formé de six décagones gauches réguliers. |  |
|
|
Icosaèdre de PETRIE formé de six décagones gauches réguliers. |
Par la suite, et à partir de polyèdres convexes "classiques" [Nous les appelons: "Polyèdres euclidiens"] (à faces planes) semblables aux polyèdres illustrés ci-après, nous avons expliqué comment, en s’appuyant sur les couleurs des faces et la relation d'incidence "Toute arête est à l'intersection de deux faces" ou "Toute arête est incidente à deux faces", les élèves ont calculé (dénombré) le nombre de faces, d'arêtes et de sommets des polyèdres.
A titre d'exemples, citons les cas de l'icosaèdre régulier et de l'antiprisme hexagonal.
L’ICOSAEDRE REGULIER
|
|
|
 |
Aux 5 triangles équilatéraux rouges
correspondent 5 triangles équilatéraux verts puisque "toute arête est
incidente à 2 faces".
Aux 5 triangles équilatéraux
bleus correspondent, pour la même raison, 5 triangles équilatéraux jaunes.
Il y a donc, au total: 5 + 5 +
5 + 5 = 20 triangles équilatéraux.
Le nombre d'arêtes de l'icosaèdre est obtenu par la relation:
|
A = |
nombre de faces triangulaires x nombre de d'arêtes par face |
|
2 |
La valeur (2) du dénominateur résulte de 'toute arête est incidente à deux faces".
|
A = |
20 (faces triangulaires) x 3 (arêtes) |
= 30 arêtes |
|
2 |
Remarque: Le nombre de sommets de l'icosaèdre régulier est obtenu par la relation:
|
S = |
20 (faces triangulaires) x 3 (nombre de sommets par face) |
|
5 |
En chaque sommet s'attachent 5 faces |
L’ANTIPRISME SEMI REGULIER A BASES HEXAGONALES
|
|
 |
 |
A la base hexagonale verte,
correspondent 6 triangles équilatéraux bleus ® 7 faces ( 1 + 6 ).
A la base hexagonale rouge,
correspondent 6 triangles équilatéraux jaunes ® 7 faces aussi.
Au total, il y a donc 14 faces (2 hexagones réguliers et 12 triangles
équilatéraux)
Le nombre d'arêtes vaut donc:
| A = |
(nombre d'hexagones x 6) + (nombre de triangles x 3) |
|
2 |
La valeur (2) du dénominateur résulte de « toute arête est incidente à deux faces ».
|
A = |
(2 x 6) + (12 x 3) |
= 24 arêtes |
|
2 |
Le nombre de sommets de l'antiprisme vaut:
| S = |
(nombre d'hexagones x 6) + (nombre de triangles x 3) |
|
4 |
En chaque sommet s'attachent exactement 4 faces |
|
S = |
(2 x 6) + (12 x 3) |
= 12 |
|
4 |
Remarque: Il est évident que l'on peut déterminer aussi le nombre des sommets à partir des deux bases (6 x 2 = 12 )
Nous avons généralisé les mêmes types de raisonnements à d'autres polyèdres convexes.
L'analyse des deltaèdres [Il en existe exactement huit] convexes (polyèdres convexes dont toutes les faces sont des triangles équilatéraux) a permis d'illustrer comment familiariser des élèves, dès l' âge de 11 ans, à la notion de preuve par l'absurde.
Après avoir initié les élèves de cet âge au calcul du nombre d'arêtes de polyèdres, nous leur posons la situation - problème suivante:
"Construire un deltaèdre à partir de cinq triangles équilatéraux isométriques."
Après plusieurs tentatives
infructueuses, des élèves constatent que la construction est impossible.
Nous leur disons alors que, même sans assembler les triangles, ils peuvent
affirmer qu'il n'existe pas de polyèdre formé de 5 triangles équilatéraux
isométriques !
Nous leur suggérons d'en faire la preuve en imaginant que ce polyèdre existe.
Ainsi, si ce polyèdre existait, son nombre d'arêtes vaudrait:
|
A = |
5 x 3 |
= 7,5 |
|
2 |
Les élèves constatent alors que ce
polyèdre est "impossible" car le nombre d'arêtes doit être nécessairement
un nombre entier.
Ils découvrent encore que le nombre de faces des deltaèdres doit être un
nombre pair.
Pour les polyèdres (convexes) formés de polygones isométriques ayant un
nombre impair de côtés, ils découvrent qu'il faut aussi utiliser un nombre
pair de faces.
Thème 2.
Dans le deuxième thème: "LES TETRAEDRES A FACES ISOMETRIQUES", il s'agissait de préciser les types de triangles (A,B,C) qui permettent de construire un tétraèdre à faces isométriques.
|
|
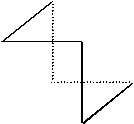
Contrairement à ce que suggèrent la relation "Toute arête est incidente à deux faces" et le développement du tétraèdre potentiel ci-dessous, il n'est pas vrai qu'il soit possible de construire un tétraèdre isométrique avec n'importe quel type de triangles.
|
|
La contrainte (souvent oubliée) de "l'inégalité angulaire" impose que les triangles isométriques soient des triangles acutangles.
En effet, cette inégalité angulaire affirme que l'amplitude d'un des angles « déterminant » un sommet d’un polyèdre doit être inférieure à la somme des amplitudes de tous les autres angles-faces « déterminant » ce même sommet. (Cette inégalité angulaire est analogue à la fameuse inégalité polygonale [Dans tout polygone, la longueur d’un côté est inférieure à la somme des longueurs de tous les autres côtés.].)
Pour notre problème, l'inégalité angulaire impose donc:
 < B + Ĉ = 180° -  Þ
 < 90°
B < Â + Ĉ = 180° - B Þ
B < 90°
Ĉ < Â + B = 180° - Ĉ Þ
Ĉ < 90°
Il en résulte donc que: "Les triangles isométriques admissibles doivent être acutangles."
Remarque : Dans un tétraèdre à faces isométriques, la somme des amplitudes des angles-faces « déterminant » un sommet vaut toujours 180°.
Voici quelques photos illustrant une partie du matériel didactique utilisé en classe et présenté à Pau ainsi que deux photos des participants .
 |
 |
 |
 |
 |
 |
 |
 |