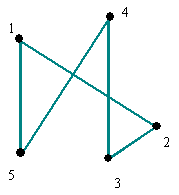
Plan des activités de QUATRIEME ANNEE PRIMAIRE
Thème 1 : Figures géométriques planes fermées
Classements des figures géométriques en polygones, non-polygones (figures rondes, figures hybrides).
Maîtrise des quantificateurs: "pour tout »; « il existe ».
Maîtrise de la conjonction "et".
Négation orale d’un « pour tout », d’un « il existe « et de la conjonction « et ».
Représentations des classements sous forme de diagrammes.
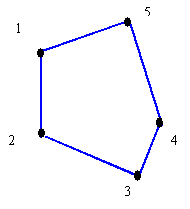
Traçage de polygones en suivant la numérotation des sommets.

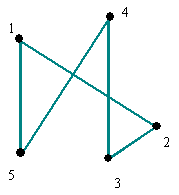
Construction de polygones avec des segments de droite dessinés sur transparents.
Fixation de la relation existant entre le nombre de côtés, de sommets et d’angles des polygones.
Exercices individuels.
Thème 2 : Solides géométriques
Classement des solides géométriques, en fonction de la forme de leurs faces, en polyèdres et non-polyèdres (corps ronds, corps hybrides).
Correspondance entre des solides géométriques, leurs photos prises sous des angles différents et leurs dessins en perspective cavalière.
Représentations du classement des solides géométriques sous forme de diagrammes.
Distinction de polygones et de polyèdres.
Correspondance existant entre le classement des figures géométriques et le classement des solides géométriques.
Détermination raisonnée du nombre de faces, d’arêtes et de sommets de polyèdres : cube, tétraèdre régulier, icosaèdre régulier, dodécaèdre régulier.
Essai de construction de polyèdres à faces triangulaires (deltaèdres) avec un nombre impair de faces (raisonnement par l'absurde).
Classement de polyèdres en fonction du nombre de faces.
|
|
|
|
Calcul du nombre de chalumeaux (pailles) nécessaires à la construction de quelques polyèdres imposés.
Construction de polyèdres en chalumeaux, semblables à des polyèdres réalisés en plaquettes POLYDRON.
Exercices individuels.
Thème 3 : Transformations du plan – Similitudes planes
Figures déformées - Figures non déformées
Figures non déformées (semblables ou proportionnelles)
Figures semblables agrandies - Figures semblables réduites - Figures isométriques
Figures isométriques ou figures physiquement superposables
Figures superposables (isométriques) par déplacement et /ou par retournement - notion d'orientations du plan (dessins de main gauche, dessin de main droite, sens horlogique et sens antihorlogique).
Notion de symétries au sens large (automorphismes) : déplacement et /ou retournement qui superpose(nt) une figure à elle- même.
Exercices individuels.
Thème 4 : Les angles
Rappel des différents types d'angles: droit, aigu, obtus, plat, plein, nul (manipulations et psychomotricité).
Mesurage de l’amplitude de l’angle droit et d’angles plus écartés ou moins écartés que l’angle droit.
Angles intérieurs de polygones convexes et non convexes.
Angles opposés formés par des droites sécantes.
Angles alternes et internes associés à deux droites parallèles.
Somme des angles intérieurs d'un triangle (180 degrés).
|
|
Exercices individuels: repérage d’angles droits, d’angles aigus, d’angles obtus ; traçage d’angles imposés, mesurage de l’amplitude d’angles donnés et calcul de la valeur des angles complémentaires.
Thème 5 : Droites, segments de droites et milieu d'un segment de droite
Comparer droite et segment de droite.
Caractéristiques des segments de droites.
Droites sécantes – Droites concourantes
Mesurer des segments de droites – représentation symbolique de segments de droites.
Milieu d'un segment de droite dans le plan et dans l’espace.
Milieu d'un segment de droite du plan et transformations.
Segments de droite se coupant en leur milieu.
Exercices individuels
Thème 6 : Les orientations du plan
Les deux orientations du plan - sens horlogique et sens antihorlogique.– figures orientées – dessins de mains et dessins de pieds.

Thème 7 : Les cercles
Cercles et disques – corde , diamètre, rayon, centre.
|
|
« Définition » d’un cercle.
Points « frontière », points extérieurs, points intérieurs d’un cercle et distance par rapport au centre.
Cercles concentriques.
Exercices individuels.
Thème 8 : Les rotations dans le plan
Rosaces et rotations (approche visuelle).
Premières caractéristiques liées aux rotations (déplacements – amplitudes de la rotation - sens de la rotation – centre de la rotation « point fixe »).
Positionnement approximatif de figures (sur transparents) par des rotations données.
|
|
Fractions de tour et angles balayés.
Détermination des rotations qui superposent des figures à elles- mêmes (carrés, rectangles quelconques, losanges quelconques, parallélogrammes quelconques).
Exercices individuels.
Thème 9 : Les symétries orthogonales du plan
Symétries orthogonales (approche visuelle).
Premières caractéristiques liées aux symétries orthogonales (retournement – inversion de l’orientation - droite de points fixes – « perpendiculaires – mêmes distances»).
« Figures vertes = images des figures rouges par la symétrie orthogonale plane d’axe bleu ».
|
|
Cliquez ici pour voir les remarques à propos des symétries orthogonales planes et du pliage |
Image d’un point par une symétrie orthogonale donnée.
Positionnements approximatifs de figures (sur transparents) par des symétries orthogonales données.
Détermination de symétries orthogonales qui superposent les figures à elles-mêmes (carrés, losanges quelconques, rectangles quelconques, parallélogrammes quelconques, cercles …).
Axes de symétrie (médianes et diagonales de quadrilatères – autres figures).
Exercices individuels
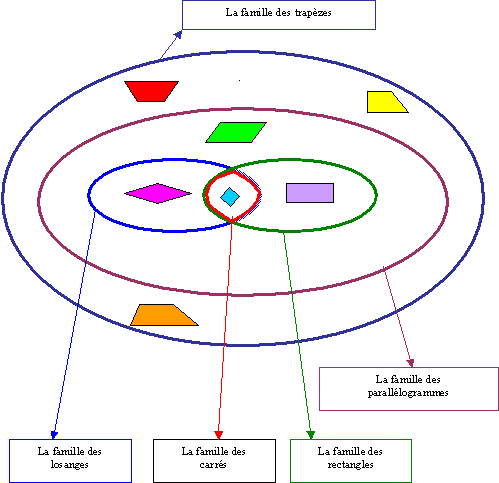
Thème 10 : Les familles de quadrilatères
Il s’agit de prolonger l’approche réalisée en troisième année primaire.
|
|
A. La famille des carrés.
B. La famille des rectangles.
C. La famille des losanges..
D. La famille des parallélogrammes.
E. La famille des trapèzes
|
Thème 11 : Les rosaces
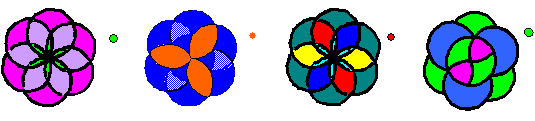
Rechercher les rotations qui superposent des rosaces à elles–mêmes.
Colorer des rosaces en tenant compte des contraintes imposées.
Construire, aux instruments, des rosaces d’après des procédés imposés.
Créer des rosaces différentes par le choix et la régularité des coloriages
|
|
| Retour à 'Plans du cours |
La
notion de pliage est devenue un concept fondamental en sciences méritant un développement
plus important en didactique mathématique.
En effet, le pliage est lié aux théories [1]
se rapportant aux origamis, aux airbags, aux lentilles de télescopes spatiaux,
aux protéines, aux immeubles de Jacques TITS …
Néanmoins et bien que en relation indirecte avec les symétries orthogonales
planes, nous attirons l’attention sur le fait que le pliage d’une feuille de
papier n’est pas, à nos yeux pour l’enseignement élémentaire, le premier
modèle concret à utiliser pour illustrer la notion de symétrie orthogonale
dans le plan.
En effet, le pliage d’une feuille de papier ne permute pas en même temps les
deux demi-plans déterminés par la droite de points fixes de la symétrie
orthogonale. Le pliage d’une feuille de papier n’applique pas toujours une
droite sur une droite ; toujours un segment sur un segment ; une
diagonale d’un rectangle sur l’autre diagonale de ce rectangle lorsque la
droite de points fixes de la symétrie orthogonale est une des deux médianes de
ce rectangle…
Bref, pour la Géométrie élémentaire des Transformations, le pliage d’une
feuille de papier ne permet pas aux enfants d’observer que certaines figures
sont superposables à elles-mêmes par symétrie orthogonale plane ;ni de
se constituer une image mentale correcte des notions conservées par ce type de
transformations. Or, ces notions sont fondamentales pour comprendre la structure
des figures
en géométrie actuelle. Pour pallier à cet inconvénient, nous « retournons »
un transparent qui « recouvre toute la feuille de papier sensée représenter
un plan ».
Cet « outil » permet alors de montrer :
la permutation simultanée des deux demi-plans situés de part et d’autre de la droite définissant une symétrie orthogonale plane ;
que l’image de toute droite est une droite ;
que l’image de tout angle est un angle ;
que l’image de tout cercle est un cercle ;
que l’image de tout segment est un segment ;
que tout rectangle est superposable à lui-même par au moins deux symétries orthogonales planes ;
que des figures sont superposables à elles-mêmes par symétrie orthogonale ;
Ajoutons pour terminer que la transformation "simple pliage d’une feuille de papier" est une transformation qui ne conserve pas les distances. Ce simple pliage ne modélise donc pas une symétrie orthogonale plane qui, elle, conserve les distances.
[1] Informations fournies par Francis BUEKENHOUT (U.L.B.)