Plan des activités de CINQUIEME ANNEE PRIMAIRE
Thème 1 : Figures géométriques planes fermées
Classements des figures géométriques en polygones, non-polygones (figures rondes, figures hybrides).
Maîtrise des quantificateurs: "pour tout »; « il existe ».
Maîtrise de la conjonction "et".
Négation orale d’un « pour tout », d’un « il existe « et de la conjonction « et ».
Représentations des classements sous forme de diagrammes.
Traçage de polygones en suivant la numérotation des sommets.
Création des trois types de figures géométriques
Fixation de la relation existant entre le nombre de côtés, de sommets et d’angles des polygones.
Etablissement de la synthèse à retenir à propos des « définitions » et des remarques concernant les figures géométriques ;
Exercices individuels.
Thème 2 : Solides géométriques
Classement des solides géométriques, en fonction de la forme de leurs faces, en polyèdres et non-polyèdres (corps ronds, corps hybrides).
Correspondance entre des solides géométriques, leurs photos prises sous des angles différents et leurs dessins en perspective cavalière.
Représentations du classement des solides géométriques sous forme de diagrammes.
Distinction de polygones et de polyèdres.
Etablissement de la correspondance existant entre des figures géométriques et des faces de solides.
Correspondance existant entre le classement des figures géométriques et le classement des solides géométriques
Etablissement de la synthèse à retenir à propos des « définitions » et des remarques concernant les solides géométriques;
Dénombrement raisonné des faces de divers polyèdres : polyèdres platoniciens, deltaèdres, prismes et antiprismes, pyramides
|
|
|
|
Prisme |
Antiprisme |
Découverte de la généralisation du dénombrement des faces des prismes.
Découverte de la généralisation du dénombrement des faces des pyramides.
Sélection des polyèdres dont toutes les faces sont isométriques.
Parmi les polyèdres dont toutes les faces sont isométriques, recherche de ceux qui sont homogènes en leurs sommets (les polyèdres réguliers).
Dénombrement raisonné des arêtes et des sommets des polyèdres réguliers, de prismes, d’antiprismes et de pyramides
Thème 3 : Transformations du plan – Similitudes planes
|
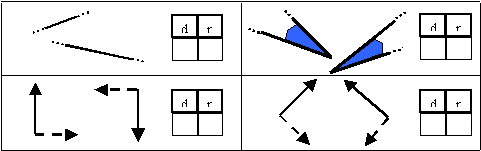
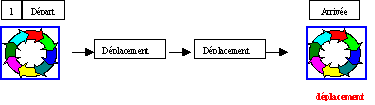
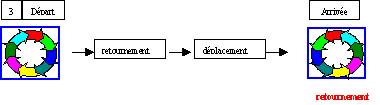
Figures superposables à elles-mêmes par déplacement(s) et/ou par retournement(s) du plan
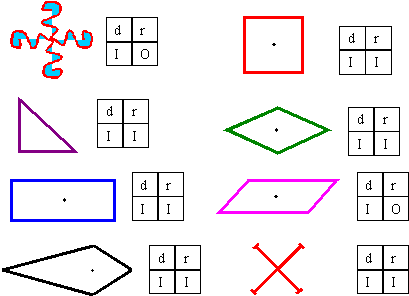
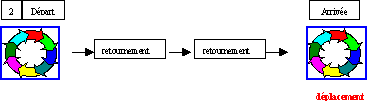
Notions
conservées par les déplacements et les retournements du plan
Les deux orientations du plan (rappel) :
- sens horlogique et sens antihorlogique
- dessins de mains
Les
premières notions conservées par un déplacement et par un retournement (comparer
ce qui varie et ce qui ne varie pas)
Compositions (pairezs ou impaires) de déplacements et/ou de retournements du plan
Thème 4 : Droites - Segments de droites
Droites :
Représentation
de droites verticales ; droites horizontales ; droites obliques.
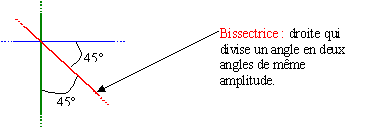
Représentation d’une droite oblique inclinée à 45° par rapport à une
droite horizontale (première notion de bissectrice)
Droites et points :
Tracer toutes les droites qui peuvent passer par un seul point donné.
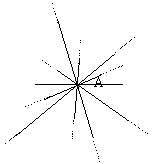
Remarquer
qu’il existe une infinité de droites passant par un seul point et que toutes ces droites recouvrent tout le plan.
que le plan est illimité dans toutes les directions.
Faire tracer toutes les droites pouvant passer par les deux points distincts et remarquer que par deux points distincts passe une et une seule droite.
Faire tracer toutes les droites passant par les
trois points distincts donnés
Remarquer : il
passe une et une seule droite par deux point distincts
Faire tracer toutes les droites passant par trois points distincts et distinguer les différents cas.
Faire tracer toutes les droites passant par quatre points donnés et distinguer les différents cas.
Faire rechercher comment on peut obtenir 7 points distincts alignés ? et 8 ? et 10 ? et plus encore ?
Faire imaginer un point de l’espace et rechercher
combien de droites passent par ce point de l’espace.
Découvrir qu’une infinité de droites passent par le point donné.
Découvrir qu’elles remplissent tout l’espace.
Faire imaginer deux points de l’espace et combien
de droites passent par ces deux points de l’espace.
Découvrir
qu’il ne passe qu’une et une seule droite par deux points de l’espace
Segments de droite :
Faire représenter un segment de droite [A B] et faire remarquer :
qu’un segment de droite est limité dans les deux sens.
qu’un segment de droite ne contient pas de trou, il est continu.
Faire partager exactement un segment de droite en deux demi-segments de même longueur en utilisant le compas (première notion de médiatrice)
| Jeu du milieu (dans l'espace et dans le plan) |
|
Exercices individuels :
Reconnaître des droites et des segments de droite ; faire tracer des
segments de droite de même longueur et des segments de droite de longueurs différentes
imposées.
Faire partager exactement des segments de droite en deux demi-segments de même
longueur, en utilisant le compas.
Sans latte, vérifier si des segments de droite sont
de même longueur ; s’ils sont superposables et comment (par déplacement
et/ou par retournement).
Vérifier si des droites sont superposables (par déplacement et/ou par
retournement).
Positions relatives de deux droites dans le plan (et dans l'espace)
Positions relatives
de deux droites
Droites parallèles à une droite ; droites perpendiculaires à une droite
Médiatrice d’un segment (tracer et définir)
|
|
|
|
Thème 5 : Les angles
Rappel :
Définitions
Types d’angles
Angles superposables
Raisonner à partir des angles
|
|
|
|
|
Thème 6 : Cercles et disques
|
|
Thème 7 : Déplacement particulier du plan : Les rotations
|
|
Thème
8 :
Retournement particulier du plan : Les symétries orthogonales
(Notions conservées ou non
conservées par les déplacements et par les retournements du plan)
|
|
Thème 9 : Médianes et diagonales des quadrilatères
|
|
Thème 10 : Les frises
Réalisation de frises du type déplacements et symétries glissées
Travail collectif puis travaux individuels
|
|
|
| Retour à 'Plans du cours' |