Géométrie des Transformations

Retour à 'Plans du cours'  

Plan des activités de SIXIEME ANNEE PRIMAIRE

Thème 1 : "Remise en route générale"

Mesurer des angles donnés (aigus, obtus); tracer des angles d'amplitudes imposées (avec l'équerre Aristo); calculer l'amplitude  d'angles complémentaires et d'angles supplémentaires.

Figures superposables à elles-mêmes ( ou recherche des automorphismes): droites, segments de droites, droites orientées, droites sécantes, droites parallèles, angles, figures "non géométriques", figures géométriques (surtout les quadrilatères), dessins orientés (cercles orientés et dessins de mains).

Recherche de symétries orthogonales possibles dans des figures (ou axes de symétrie de ces figures).

Tracer les médianes des quadrilatères.

Tracer les diagonales des quadrilatères.
 

	Recherche de tous les points situés à une distance donnée d'un point. Recherche de tous  les  points situés à une distance donnée de deux points distincts (médiatrice d'un segment).
Recherche de l'orbite d'un point dans un carré, par les automorphismes du carré (ses  rotations et ses symétries orthogonales).

Haut de la page

Thème 2 : droites - segments de droites

Droites Positions relatives  de deux droites: parallélisme et perpendicularité  Segments de droites Milieu d'un segment de droite

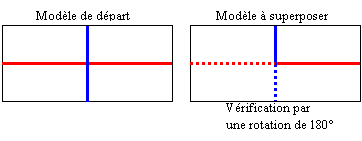Segments de droite  se coupant en leur milieu

Haut de la page

Thème 3 : Propriétés des médianes et des diagonales des quadrilatères

Des carrés Des rectangles quelconques Des losanges quelconques Des parallélogrammes quelconques Des trapèzes quelconques Des quadrilatères quelconques du type: cerfs-volants De tous les quadrilatères repris ensuite "famille par famille"
	Sont-elles de même longueur? Se coupent-elles en leur milieu? Sont-elles perpendiculaires? Sont-elles des axes de symétrie ? (Vérification à l'aide des transformations)

Exercices de réinvestissements et prolongements; exemples:

Connaissant les caractéristiques des diagonales, reconnaître les quadrilatères correspondants
	Construire des parallélogrammes connaissant la longueur d'un côté, l'amplitude d'un angle et la longueur d'une diagonale.

Haut de la page

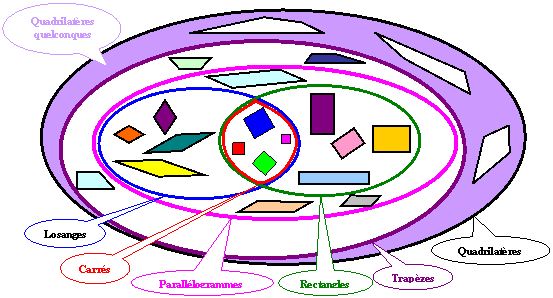
Thème 4 : Classement des quadrilatères (convexes) - famille par famille

La famille des carrés; la famille des losanges, la famille des rectangles, la famille des parallélogrammes, la famille des trapèzes, la famille des quadrilatères quelconques.

Rappel et mise au point pour chaque famille: 

1. Quelles sont leurs caractéristiques?

2. Combien en existe-t-il?

3. Sont-ils tous semblables?- Détermination des différents types existants.

4. Quelles sont les transformations qui les superposent à eux-mêmes?

5. Quelles sont les qualités communes à tous les membres d'une même famille?

6. Représentations des familles. 

Elaboration de toutes les synthèses à retenir

Haut de la page

Thème 5 : Classement des triangles

Rappel ou (re)découverte de la somme des angles de tout triangle: a)    par le découpage et le collage. b)    par le parallélisme (angles alternes/internes). Premier classement des triangles a)    en fonction de la LONGUEUR DES CÔTES. b)    en fonction de l'AMPLITUDE DES ANGLES.  c)    en fonction des deux critères suivants:  "longueur des côtés "et "amplitude des angles " Différenciation des triangles: isocèles, équilatéraux, rectangles, rectangles isocèles, quelconques.

Recherche des transformations permettant de superposer chaque type de triangle à lui-même. 

Exemples:

Classement des triangles famille par famille.

Recherche des propriétés communes à tous les membres d'une même famille.

Exercices de manipulations et exercices de réflexion:  

-        Faisabilité de triangles (avec quelles longueurs de segments?) 

-        Calcul d'angles en fonction du type de triangle

Problèmes de réinvestissement des acquis nécessitant l'argumentation:

• "Qu'est-ce que je" reçois" dans l'énoncé du problème ? "

• "Qu'est-ce que je cherche ?" 

• "De quelles connaissances dois-je me servir?" - argumentation et vérification.

Achever des constructions données, au départ d'angles et en tenant compte du type de triangles

Constructions imposées:

• au compas 

• au départ du rapporteur de l'équerre Aristo 

Haut de la page

Thème 6 : Figures géométriques et solides géométriques

Rappel des définitions et du classement des figures géométriques: polygones – figures hybrides – figures rondes.

Première approche de polygones convexes réguliers. 

Rappel du classement des polyèdres en fonction de la régularité des faces et de l'homogénéité des sommets.

Différenciation de pyramides - prismes – antiprismes – autres.

Dénombrement des faces de polyèdres.

Rappel du calcul des faces, des arêtes et des sommets de polyèdres à faces régulières et homogènes en leurs sommets.

A l'aide du matériel POLYDRON, rechercher les 11développements du cube.

Dans les 11 développements, colorier d'une même couleur, les faces parallèles.

Associer des développements de solides à leur représentation en perspective cavalière.

Tracer aux instruments un développement de parallélépipède rectangle.

Représenter un cube en perspective cavalière.

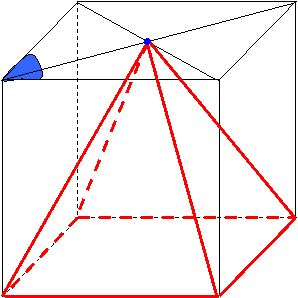
Représenter un cube et une pyramide dans un cube (en perspective cavalière).

Repérer la hauteur d'une pyramide.

Thème 7 : Repérage de points dans un système d'axes

Sur un modèle donné et en se servant des axes horizontal et vertical, donner les coordonnées de quelques points imposés.

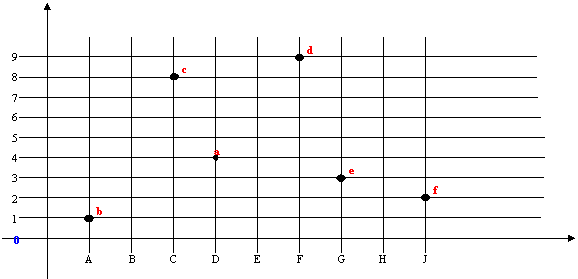
Les coordonnées de quelques points sont données, situer ces points dans un système d'axes.

Thème 8 : Frises

Réinvestissement des acquis:  reconnaissance des types de frises donnés (à l'aide de dessins sur transparents et par superposition);  soit: Uniquement des translations (déplacements parallèles);  Des rotations (déplacements qui tournent autour de centres);  Des symétries orthogonales (retournements selon des axes de points fixes);  Des symétries glissées (symétries orthogonales + translations). Réalisation de frises individuelles selon des modèles imposés.